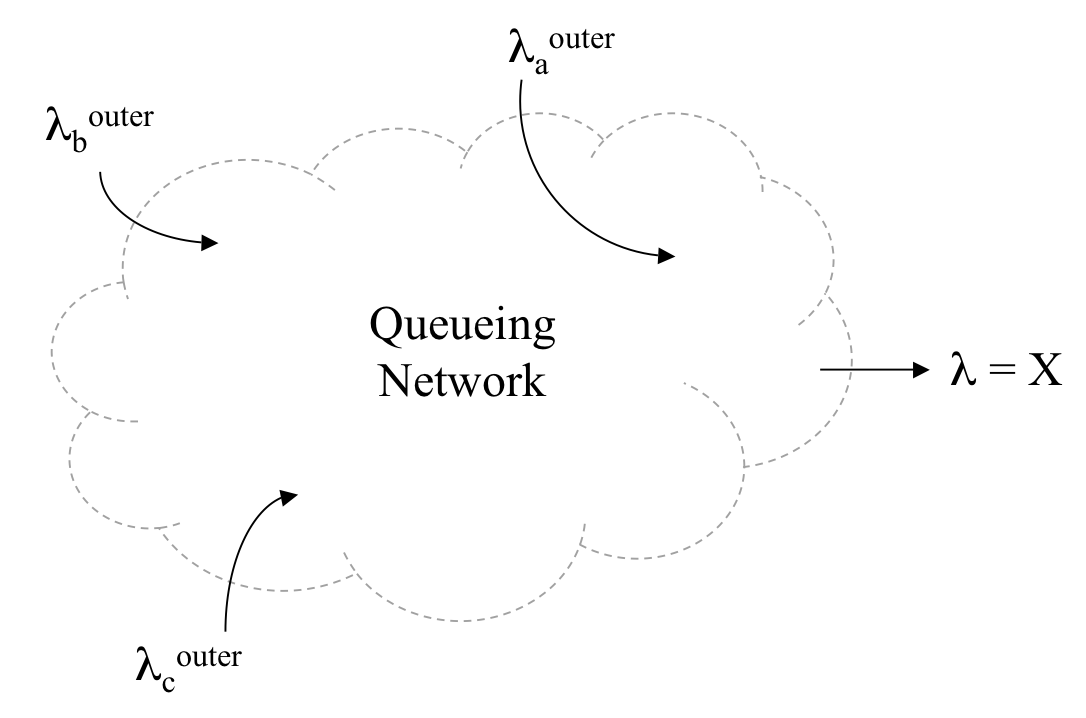
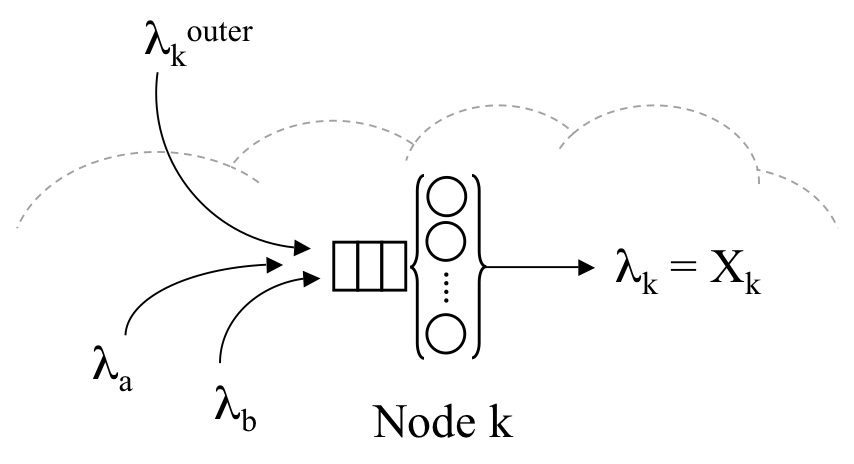
| Version: | 4.B |
| Build: | 041807 |
| Languages: | C only |
| Compiled: | gcc version 4.0.0 20041026 |
| Maintainer: | Neil Gunther |
 | If you weren't invited to come to this page, you probably shouldn't be here. In any case, caveat lector. If you were invited, you should install the beta PDQ library in a separate directory so that nothing in PDQ 4.2 gets clobbered. Visit this page early and often and do a browser Refresh to see changes (Section 2) based on the results of other beta testers 1. |  |
 Of course, there's nothing new in computer science (or performance analysis).
In 1917
Agner Erlang
studied "threaded servers" for the "Internet" of his day.
His "Internet" was the telephone network and his "threads" were trunk lines
for making calls outside Copenhagen. Trunk lines had to be reserved back then, and
the telephone company wanted to know how much trunk capacity
(measured today in Erlangs) they needed.
Erlang not only made the measurements, which showed the incoming
teletraffic calls followed a Poisson process (i.e., Exponentially
distributed interarrival periods), but he derived the very first queueing
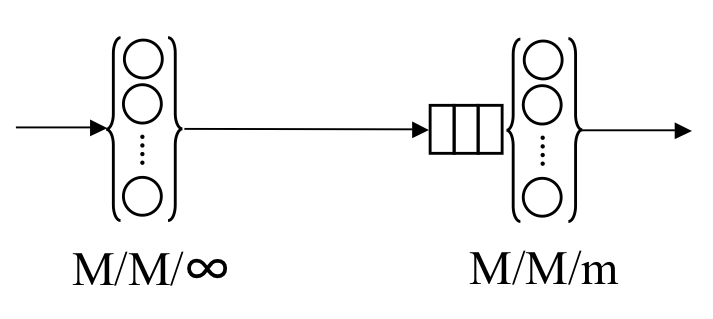
model (M/M/m, not M/M/1) in order to predict the performance (waiting time)
characteristics. Not only was the first queueing model not the simplest
model, but the application of probability theory must have appeared extremely novel back
then (less than 100 years ago).
Of course, there's nothing new in computer science (or performance analysis).
In 1917
Agner Erlang
studied "threaded servers" for the "Internet" of his day.
His "Internet" was the telephone network and his "threads" were trunk lines
for making calls outside Copenhagen. Trunk lines had to be reserved back then, and
the telephone company wanted to know how much trunk capacity
(measured today in Erlangs) they needed.
Erlang not only made the measurements, which showed the incoming
teletraffic calls followed a Poisson process (i.e., Exponentially
distributed interarrival periods), but he derived the very first queueing
model (M/M/m, not M/M/1) in order to predict the performance (waiting time)
characteristics. Not only was the first queueing model not the simplest
model, but the application of probability theory must have appeared extremely novel back
then (less than 100 years ago).