
| (1) |
| (2) |
| (3) |
| (4) |

| (5) |
| ρ | m=1 | m=2 | m=3 | m=10 |
| 0.1 | 0.1 | 0.0181818 | 0.0037037 | 1.12642 ×10−7 |
| 0.2 | 0.2 | 0.0666667 | 0.0246575 | 0.0000477373 |
| 0.25 | 0.25 | 0.1 | 0.0441176 | 0.000287631 |
| 0.5 | 0.5 | 0.333333 | 0.236842 | 0.0361054 |
| 0.7 | 0.7 | 0.576471 | 0.492344 | 0.221731 |
| 0.75 | 0.75 | 0.642857 | 0.567757 | 0.306611 |
| 0.8 | 0.8 | 0.711111 | 0.647191 | 0.40918 |
| 0.85 | 0.85 | 0.781081 | 0.730377 | 0.529861 |
| 0.9 | 0.9 | 0.852632 | 0.817061 | 0.668732 |
| 0.95 | 0.95 | 0.925641 | 0.907009 | 0.825586 |
| 0.98 | 0.98 | 0.970101 | 0.962451 | 0.928161 |
| ρ | m=1 | m=2 | m=3 | m=10 |
| 0.1 | 1.11111 | 1.0101 | 1.00137 | 1. |
| 0.2 | 1.25 | 1.04167 | 1.01027 | 1.00001 |
| 0.25 | 1.33333 | 1.06667 | 1.01961 | 1.00004 |
| 0.5 | 2. | 1.33333 | 1.15789 | 1.00722 |
| 0.7 | 3.33333 | 1.96078 | 1.54705 | 1.07391 |
| 0.75 | 4. | 2.28571 | 1.75701 | 1.12264 |
| 0.8 | 5. | 2.77778 | 2.07865 | 1.20459 |
| 0.85 | 6.66667 | 3.6036 | 2.62306 | 1.35324 |
| 0.9 | 10. | 5.26316 | 3.72354 | 1.66873 |
| 0.95 | 20. | 10.2564 | 7.04672 | 2.65117 |
| 0.98 | 50. | 25.2525 | 17.0409 | 5.64081 |
|
| (6) |
| (7) |
| (8) |
|
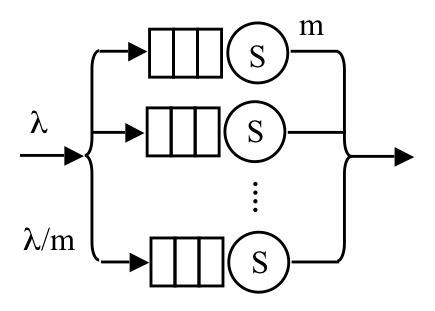
| (9) |

| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| ρ | η | 10/η | Rη | RA |
| 0 | 1 | 10 | 1 | 1 |
| 0.1 | 1.11111 | 9. | 1. | 1. |
| 0.2 | 1.25 | 8. | 1. | 1. |
| 0.3 | 1.42856 | 7.00004 | 1.00001 | 1.00001 |
| 0.4 | 1.66649 | 6.00063 | 1.0001 | 1.0001 |
| 0.5 | 1.99805 | 5.00489 | 1.00098 | 1.00098 |
| 0.6 | 2.48488 | 4.02433 | 1.00608 | 1.00608 |
| 0.65 | 2.81868 | 3.54776 | 1.01365 | 1.01365 |
| 0.7 | 3.23917 | 3.08721 | 1.02907 | 1.02907 |
| 0.75 | 3.77475 | 2.64918 | 1.05967 | 1.05967 |
| 0.8 | 4.46313 | 2.24058 | 1.12029 | 1.12029 |
| 0.85 | 5.35417 | 1.8677 | 1.24514 | 1.24514 |
| 0.9 | 6.51322 | 1.53534 | 1.53534 | 1.53534 |
| 0.95 | 8.02526 | 1.24607 | 2.49213 | 2.49213 |
| 0.99 | 9.56179 | 1.04583 | 10.4583 | 10.4583 |
| (16) |
| (17) |
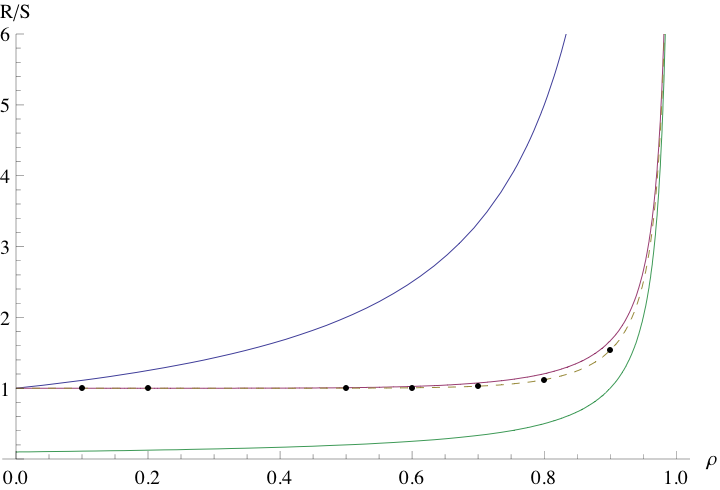
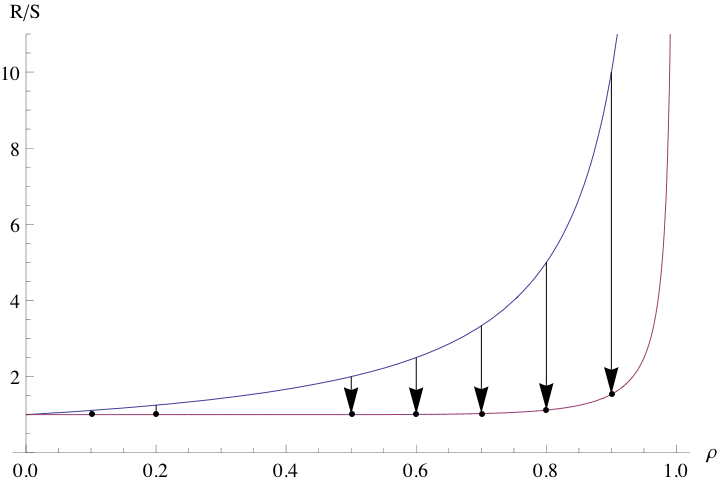
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| ρ | RE | RA | % Error |
| 0.1 | 1.00137 | 1.001 | -0.0370233 |
| 0.2 | 1.01027 | 1.00806 | -0.218699 |
| 0.3 | 1.03335 | 1.02775 | -0.541718 |
| 0.4 | 1.07843 | 1.06838 | -0.932401 |
| 0.5 | 1.15789 | 1.14286 | -1.2987 |
| 0.6 | 1.29562 | 1.27551 | -1.55217 |
| 0.65 | 1.40118 | 1.3786 | -1.61175 |
| 0.7 | 1.54705 | 1.52207 | -1.61465 |
| 0.75 | 1.75701 | 1.72973 | -1.55262 |
| 0.8 | 2.07865 | 2.04918 | -1.41781 |
| 0.85 | 2.62306 | 2.59151 | -1.20265 |
| 0.9 | 3.72354 | 3.69004 | -0.899678 |
| 0.95 | 7.04672 | 7.01139 | -0.501367 |
| 0.99 | 33.7056 | 33.6689 | -0.1089 |
| ρ | RE | RA | % Error |
| 0 | 1 | 1 | 0 |
| 0.1 | 1. | 1. | -1.2416 ×10−6 |
| 0.2 | 1.00001 | 1. | -0.000586472 |
| 0.3 | 1.00017 | 1.00001 | -0.0159397 |
| 0.4 | 1.00147 | 1.0001 | -0.136225 |
| 0.5 | 1.00722 | 1.00098 | -0.619879 |
| 0.6 | 1.02532 | 1.00608 | -1.87662 |
| 0.65 | 1.04392 | 1.01365 | -2.89985 |
| 0.7 | 1.07391 | 1.02907 | -4.17556 |
| 0.75 | 1.12264 | 1.05967 | -5.60912 |
| 0.8 | 1.20459 | 1.12029 | -6.99822 |
| 0.85 | 1.35324 | 1.24514 | -7.98864 |
| 0.9 | 1.66873 | 1.53534 | -7.99359 |
| 0.95 | 2.65117 | 2.49213 | -5.99887 |
| 0.99 | 10.6374 | 10.4583 | -1.68363 |
| ρ | RE | RA | % Error |
| 0 | 1 | 1 | 0 |
| 0.1 | 1. | 1. | -3.5527 ×10−13 |
| 0.2 | 1. | 1. | -6.4666 ×10−8 |
| 0.3 | 1. | 1. | -0.0000380073 |
| 0.4 | 1.00002 | 1. | -0.00220676 |
| 0.5 | 1.00037 | 1. | -0.037202 |
| 0.6 | 1.00302 | 1.00004 | -0.297128 |
| 0.65 | 1.00715 | 1.00018 | -0.692049 |
| 0.7 | 1.01559 | 1.0008 | -1.45678 |
| 0.75 | 1.03209 | 1.00318 | -2.8006 |
| 0.8 | 1.06402 | 1.01166 | -4.92056 |
| 0.85 | 1.12835 | 1.04032 | -7.80161 |
| 0.9 | 1.27538 | 1.1384 | -10.7404 |
| 0.95 | 1.7554 | 1.55881 | -11.1991 |
| 0.99 | 5.73933 | 5.4917 | -4.31472 |
| ρ | RE | RA | % Error |
| 0 | 1 | 1 | 0 |
| 0.1 | 1. | 1. | 0. |
| 0.2 | 1. | 1. | 0. |
| 0.3 | 1. | 1. | 0. |
| 0.4 | 1. | 1. | -3.4956 ×10−10 |
| 0.5 | 1. | 1. | -1.3324 ×10−6 |
| 0.6 | 1. | 1. | -0.000404175 |
| 0.65 | 1.00004 | 1. | -0.00361036 |
| 0.7 | 1.00023 | 1. | -0.0229767 |
| 0.75 | 1.00111 | 1. | -0.111269 |
| 0.8 | 1.00438 | 1. | -0.435968 |
| 0.85 | 1.01495 | 1.00003 | -1.46965 |
| 0.9 | 1.04854 | 1.00118 | -4.51682 |
| 0.95 | 1.18375 | 1.03899 | -12.2294 |
| 0.99 | 2.41554 | 2.10791 | -12.7355 |
| ρ | RE | RA | % Error |
| 0 | 1 | 1 | 0 |
| 0.1 | 1. | 1. | 0. |
| 0.2 | 1. | 1. | 0. |
| 0.3 | 1. | 1. | 0. |
| 0.4 | 1. | 1. | 0. |
| 0.5 | 1. | 1. | -2.0206 ×10−12 |
| 0.6 | 1. | 1. | -1.1883 ×10−7 |
| 0.65 | 1. | 1. | -7.2607 ×10−6 |
| 0.7 | 1. | 1. | -0.000216284 |
| 0.75 | 1.00004 | 1. | -0.00354116 |
| 0.8 | 1.00036 | 1. | -0.035532 |
| 0.85 | 1.00244 | 1. | -0.243851 |
| 0.9 | 1.01319 | 1. | -1.30205 |
| 0.95 | 1.07153 | 1.00141 | -6.54384 |
| 0.99 | 1.67795 | 1.3817 | -17.6558 |
| (23) |
| (24) |
| (25) |
| (26) |
|
| (27) |
| (28) |
| (29) |